2024金融工程行业报告：CTGAN优化资产配置策略

1引言

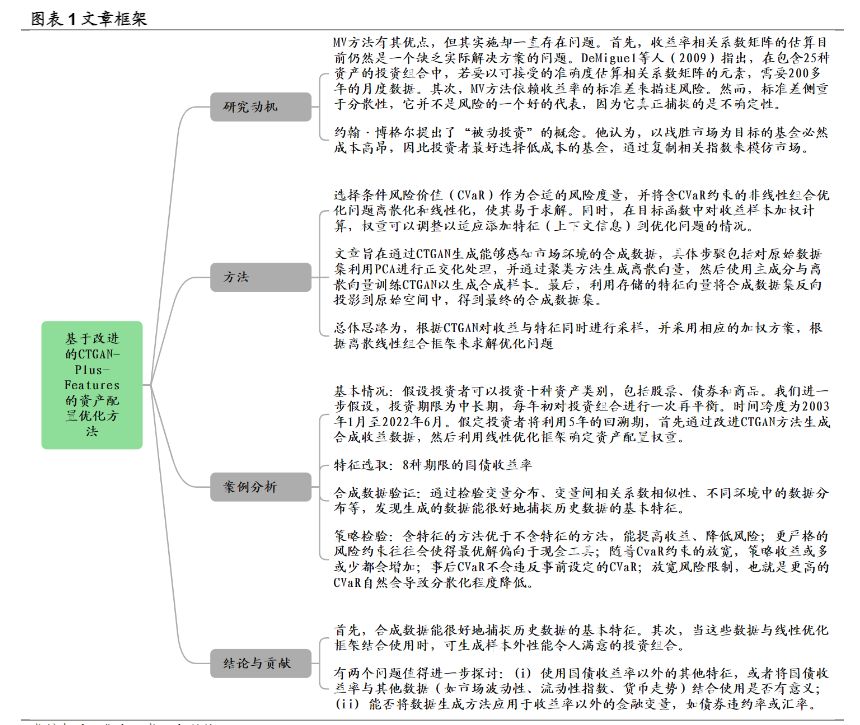
投资组合选择问题——如何将给定预算分配给多个资产——可能是金融学中最古老的问题之一。1952年，马科维茨发表了著名的投资组合选择论文，在此之前，人们一直在用感觉、直觉和常识来解决这个问题，而这些方法在本质上都是定性的。马科维茨的开创性工作表明，投资组合选择问题本质上是一个优化问题，可以在一个定义明确的数学框架内加以阐述（Markowitz, 1952）。

这一框架背后的关键思想（如分散投资的重要性、风险与收益之间的权衡以及有效边界）经受住了时间的考验。不仅如此，马科维茨的论文还引发了对这一主题的大量定量研究，标志着与过去工作相比的重要转变。然而，尽管马科维茨方法（也称为均值-方差或MV投资组合）有其优点，但其实施却一直存在问题。首先，收益率相关系数矩阵的估算——MV公式的重要支柱——是一个仍然缺乏实际解决方案的问题。例如，DeMiguel、Garlappi和Uppal（2009）得出的结论是，在包含25种资产的投资组合中，若要以可接受的准确度估算相关系数矩阵的元素，需要200多年的月度数据。马科维茨公式的第二个缺点是依赖收益率的标准差来描述风险。然而，标准差侧重于分散性，它并不是风险的一个好的代表，因为它真正捕捉的是不确定性——这是一个微妙但重要的区别（Friedman et al., 2014）。

无论如何，在上个世纪下半叶，大多数研究工作都致力于设计出实用的策略来实现MV公式，这些工作的成功程度也是参差不齐的，而如今大多数从业者已不再局限于最初的马科维茨方法。Kolm、Tütüncü和Fabozzi（2014）很好地总结了与实施马科维茨方法所面临的挑战。Pagnoncelli、Ramírez、Rahimian和Cifuentes（2022）简要概述了对试图解决MV理论在实践中所遇到问题的不同技术。约翰·博格尔是另一位先驱者，他创立了资产管理公司Vanguard Group，被公认为指数投资的奠基人。

1975年，他提出了“被动投资”的概念。他认为，以战胜市场为目标的基金必然成本高昂，因此投资者最好选择低成本的基金，通过复制相关指数来模仿市场（Bogle, 2018; Thune, 2022）。这一创新在当时备受争议，但一项又一项研究表明，在流动性和公开市场的背景下试图战胜市场是非常困难的（Eltonet al., 2019; Fahlinget al., 2019; Sharpe, 1991; Walden, 2015）。但博格尔的想法还产生了另一个重要的影响，使得投资组合选择问题变得更容易解决：将重点从资产选择转移到资产配置。

更重要的是，在指数基金出现之前，投资者如果想投资美国股市——暂且不谈MV理论的缺点——将面临一个难以解决的大规模优化问题（如果将可行集限制为标准普尔500指数中的股票，则至少有500种选择）。如今，同样的投资者只需在每个市场中选择一个指数基金，然后集中精力估算适当的资产配置比例，就能获得更加多样化的投资组合，例如，由美国股票、新兴市场股票、高收益债券和大宗商品组成的投资组合，简而言之，这是一个小得多的优化问题（Amencet al., 2001; Gutierrezet al., 2019; Ibbotson, 2010）。无论如何，从资产选择转向资产配置，再加上上世纪末出现的、并在近几年获得广泛认可的一系列创新，在很大程度上改变了投资组合选择的格局。

在这些创新中，我们认为有以下几点：

（1）条件风险价值CVaR已成为首选的风险度量指标。其关键优势在于，它比标准差更能捕捉所谓的尾部风险，即极端事件的危险。第二个优势是，它关注的是损失而不是收益的波动性，更符合投资者表达风险偏好的方式（Rockafellar and Uryasev, 2000; Rockafellar and Uryasev, 2002）。第三个优势是，在投资组合优化问题离散化和线性化的情况下，正如我们将在下一节看到的，CVaR对用来建模收益模型的概率分布类型没有任何限制。

（2）依靠合成数据模拟现实场景的好处对于解决诸如马科维茨所描述的随机优化问题至关重要。正如Fabozzi、Fabozzi、Lópezde Prado和Stoyanov（2021）所提到的，金融建模人员在查看过去的收益数据时，只能看到单一实现路径（一个收益时间序列）的结果，但对这些时间序列背后的随机（数据生成）过程却一无所知。此外，任何旨在生成真实合成数据的方法都必须捕捉数据的实际边际分布和联合分布，即所有其他可能发生但未观察到的收益时间历史。幸运的是，神经网络和机器学习的最新进展——例如，一种称为生成对抗网络（GAN）的算法——已在许多应用中证明了其有效性（Goodfellow et al., 2014）。此外，一些作者还探索了在投资组合优化问题中应用基于GAN的算法，但其框架与本文讨论的框架不同（Lu and Yi, 2022; Mariani et al., 2019; Punet al., 2020; Takahashiet al., 2019; Lommerset al., 2021）。Eckerli等人（2021）很好地概述了机器学习尤其是GAN应用于金融研究时所面临的挑战和机遇。

（3）从业人员一致认为，一组资产的联合行为会在不同的市场环境中波动（Hamilton, 1988; Schaller andNorden, 1997）。考虑到这一观察结果，合成数据生成器（SDG）必须能够解释这一现象。换句话说，它们必须能够生成属于不同市场环境的数据，遵循多模式随机过程。

（4）在许多优化问题的表述中加入特征（上下文信息）具有重要优势。例如，Ban和Rudin（2019）的研究表明，与传统方法相比，在经典的新闻供应商问题中加入特征后，解决方案的样本外表现要好得多。其他作者也验证了在其他优化问题中加入特征的有效性（Bertsimas andKallus,2020; Chenet al., 2022; Huet al., 2022; See andSim, 2010）。

在此背景下，我们的目标是提出一种基于资产配置的投资组合选择方法。具体来说，我们假设投资者具有中长期的投资视角，可以通过指数基金参与多个流动和公开市场。这样，问题简化为在假设再平衡的频率不高的情况下，估算适当的投资组合权重。在本研究中，我们假设每年进行一次再平衡。如果每天、每周或每月再平衡投资组合，显然有悖于被动投资的初衷，同时会产生过高的交易成本，最终可能影响投资业绩。

我们的方法将基于与MV方法类似、但受CVaR风险约束的框架。更重要的是，该框架将依赖于使用改进后的条件生成对抗网络（GAN）方法生成的合成收益数据，并通过融合上下文信息（在本案例中为美国国债收益率曲线）加以增强。从某种意义上说，我们的方法借鉴了Pagnoncelli等人（2022）的思想，但在几个关键方面有所不同，并带来了重大优势，包括性能方面的优势，我们将在后续部分详细讨论这一话题。总之，我们的目标有两个方面。

首先，我们提出一种有效的合成数据生成算法；其次，我们将这种算法与上下文信息相结合，提出一种资产配置方法，理想情况下，这种方法应能产生可接受的样本外表现。在下一节中，我们将更精确地阐述当前的问题，然后详细描述合成数据的生成过程，最后给出一个数值示例。最后一节是结论部分。

2问题描述

假设投资者可以投资𝑛种资产，每种资产都有一个价格指数。我们将投资组合优化问题定义为资产配置问题，在这个问题中，投资者通过调整不同资产类别的权重，旨在最大化收益的同时将整个投资组合的风险控制在预定的容忍水平以下。金融投资中的风险概念已在文献中得到广泛的讨论，包括不同风险度量的优缺点。

根据目前的最佳实践，我们选择了条件风险价值（CVaR）作为合适的风险度量。考虑到大多数投资者（特别是中长期投资者）更注重避免损失而不是波动，因此CVaR相比标准差是更好的选择。此外，CVaR（不同于风险价值VaR）还具有一些吸引人的特点，即它是凸的且一致的（即满足次可加性）（Pflug, 2000）。

设𝑥∈𝑅𝑛是代表资产类别分配的权重决策向量，𝑟∈𝑅𝑛是各资产类别在给定期间内的收益率。假定𝑟的概率分布具有密度函数π(𝑟)，则投资组合的预期收益率可以表示为各类资产预期收益率的加权平均值，即假设投资者可以投资𝑛种资产，每种资产都有一个价格指数。我们将投资组合优化问题定义为资产配置问题，在这个问题中，投资者通过调整不同资产类别的权重，旨在最大化收益的同时将整个投资组合的风险控制在预定的容忍水平以下。

金融投资中的风险概念已在文献中得到广泛的讨论，包括不同风险度量的优缺点。根据目前的最佳实践，我们选择了条件风险价值（CVaR）作为合适的风险度量。考虑到大多数投资者（特别是中长期投资者）更注重避免损失而不是波动，因此CVaR相比标准差是更好的选择。

2.1离散化与线性化

在本节中，我们将解释非线性资产配置优化问题(2)如何被重新表述为一个线性规划问题，以及为什么这种形式在实践中是有用的。Rockafellar和Uryasev（2000）证明发现，求解优化问题(2)等同于求解以下优化问题：

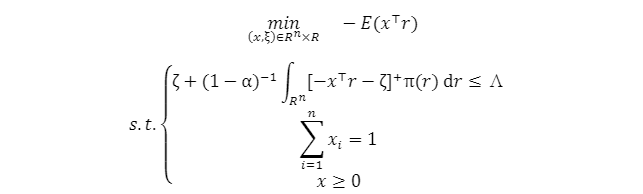
这里引入虚拟变量𝜁∈𝑅作为“损失临界值”。当环境𝜋具有离散密度𝜋𝑗时，对应的收益向量为𝑟𝑗(𝑗=1,⋯,𝑚)，则问题(5)可重新表述为

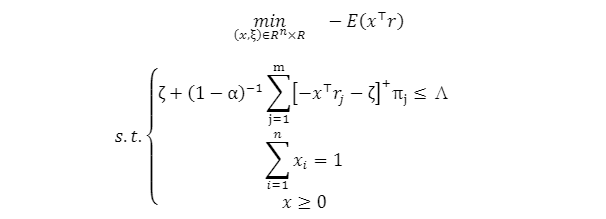
最后，引入虚拟变量𝑧𝑗，其中𝑗=1,⋯,𝑚，并将𝐸(𝑥⊤𝑟)明确写为𝑥⊤𝑅π，其中𝑅∈𝑅𝑛×𝑚表示基于密度向量𝜋的收益样本，问题(6)可以重新表述为以下线性规划问题：

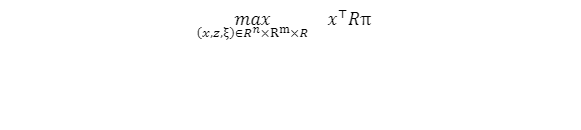
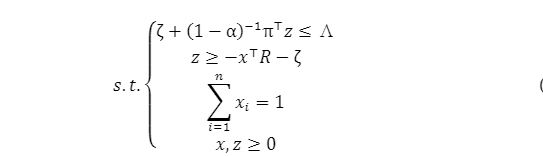
Rockafellar和Uryasev（2000）提供了等价的连续形式(5)的推导，以及后续的离散化和线性化(6)和(7)的解释与证明。Krokhmal、Uryasev和Palmquist（2002）对这些等价公式进行了深入分析，并提供了一些实例与并讨论了一般问题设置中的各种约束，如交易成本、价值约束、流动性约束和头寸限制。离散化和线性化公式(7)的优点在于它可以使用许多广泛可用的线性优化求解器进行处理。此外，离散化使我们能够将来自𝑟的相关概率分布的抽样数据与适当的离散概率密度函数π结合使用。

在本研究中，𝑅代表收益的样本分布，向量𝜋确定了𝑚个环境中样本收益向量的权重。例如，在从一组历史收益中随机不放回抽样的简单情况下，𝜋可以自然地定义为𝜋𝑗=1/𝑚,𝑗∈{1,⋯,𝑚}。然而，请注意，权重𝝅可以调整以适应添加特征（上下文信息）到优化问题的情况。例如，假设我们正在将𝑙个特征𝐹∈𝑅𝑙×𝑚合并到优化问题中。在这种情况下，我们重新定义𝜋来反映基于特征与当前经济环境的相似性所赋予的不同重要性。

3合成数据生成

原则上，从给定的概率密度函数中生成随机样本是一项相对简单的任务。但在实践中，有两大局限性使金融研究人员和从业人员无法完成这项简单的任务。首先，如前所述，金融分析师只能知道由未知随机过程生成的单条路径（一个样本结果），即由未知数据生成过程（DGP）生成的多维历史收益时间序列（Tu and Zhou, 2004）。

第二个限制因素是，所有金融变量的随机过程的非平稳性。金融体系是动态且复杂的，由于内生效应和外部因素（如监管变化、地缘政治），条件和机制随时发生变化。因此，直接依赖历史数据来生成具有代表性的假设情景，或者根据传统参数模型来生成此类假设情景的尝试都不能令人满意。因此，考虑到这些因素，我们的方法中涉及使用机器学习技术根据最近的历史数据生成合成数据。

更确切地说，根据一种能够感知市场环境地生成建模方法来生成收益率样本，这种方法被称为条件表格生成对抗网络（Conditional Tabular Generative Adversarial Networks，CTGAN）。CTGAN以无监督模式自动学习和发现历史数据中的模式，从而生成模拟未知数据生成过程的真实合成数据。然后，我们利用这些生成的合成数据，为(7)所描述的离散优化问题提供信息。简而言之，我们的目标是，在给定𝒎𝒉个样本的资产回报𝑹𝒉和特征𝑭𝒉组成的历史数据集𝓓𝒉的情况下，训练合成数据生成器（SDG）以按需合成逼真数据𝓓𝒔。图表2直观地概括了这一程序。

3.1条件表格生成对抗网络（CTGAN）

机器学习和神经网络领域的最新进展，特别是生成对抗网络（GAN）的进展，可以根据同时含有连续型和离散型的表格型数据生成制度感知的样本，这在金融工程应用中尤其有用。Xu等人（2019）提出了条件表格生成对抗网络（Conditional Tabular Generative Adversarial Networks, CTGAN）来生成合成数据，这种方法的优点在于可以创建一个逼真的合成数据生成过程，在我们的案例中，它可以捕捉资产收益和特征之间的复杂关系，同时适应于不同市场环境。

一般来说，CTGAN的架构与标准GAN在以下几个方面有所不同：

（1）CTGAN将数据集建模为一个条件过程，其中连续变量由依赖于离散变量的条件分布定义，每种离散变量的组合都定义了一个状态，该状态决定了连续变量的单变量和多变量分布。

（2）为了避免训练过程中的类别不平衡问题，CTGAN引入了条件生成器和采样训练过程的概念。条件生成器将样本的概率分布分解为给定选定变量所有可能离散值的条件分布的集合。在这种分解的基础上，可以通过对每个特定的离散状态采样来训练条件发生器，如果为条件发生器均匀地选择状态，就能避免低频状态的表示的表达能力较差。

（3）CTGAN采用模式特定的归一化改善了连续列的归一化。对于每个连续变量，该模型使用变分高斯混合模型来识别其单变量分布的不同模式，并使用基于最可能的模式的归一化值和由所用模式定义的独热向量来分解每个样本。这一过程提高了数据集用于训练的适用性，将其转换为一个更容易被网络处理的有界向量表示形式。

3.2一种改进的CTGAN-plus-features方法

为了增强基于CTGAN架构的生成状态感知的合成数据的能力，我们使用了一种无监督方法来生成离散的市场环境或状态，根据资产收益与特征进行类别划分，最终将类别标识符作为CTGAN模型所采用的状态变量。关于如何生成市场环境感知识别模型的全面讨论超出了本研究的范围。

我们只需指出，我们采用了机器学习文献中著名的降维方法，t-NSE和密度聚类法，如HDBSCAN（Campello et al., 2013）。此外，为了减少资产相关性产生的噪音，我们首先使用PCA技术对资产收益进行主成分分析。

综上所述，如图表3所示的合成数据生成过程包括以下步骤：

（1）从原始数据集𝒟ℎ开始，其中包含资产回报𝑅ℎ和特征𝐹ℎ，共𝑚ℎ个样本；

（2）使用PCA对数据集的所有变量进行正交化，以避免模型估计受到资产相关性的影响，如股票指数之间的信息存在较大的重叠。然后存储特征向量以便在生成的合成数据集上进行反向投影。

（3）生成离散向量𝐶，为每个样本分配一个类别标识符。聚类的过程包括两个步骤：（a）使用t-SNE将数据集𝒟ℎ的维数从𝑚ℎ降低到2。（b）对𝒟ℎ的二维投影应用HDBSCAN。

（4）将PCA转换后的数据集𝒟𝑝𝑐𝑎ℎ作为连续列，以及向量𝐶作为额外的离散列，训练CTGAN。

（5）使用训练过的CTGAN生成𝑚𝑠个合成样本，得到𝒟𝑝𝑐𝑎𝑠。

（6）利用存储的特征向量将合成数据集𝒟𝑝𝑐𝑎𝑠反向投影到原始空间中，得到合成数据集𝒟𝑠。

（本文仅供参考，不代表我们的任何投资建议。如需使用相关信息，请参阅报告原文。）